TD Trigonométrie et triangles
|
Les formules dont vous aurez besoin pour répondre aux questions sont dans Formulaire de trigonométrie |
✎ Travail n° 1 Pythagore 1
Un maçon réalise un marquage au sol pour délimiter une surface de 3m x 4m sur laquelle il va couler une chappe béton qu’il souhaite parfaitement rectangulaire.
Pour vérifier son tracé, il utilise le théorème de Pythagore.
🎯 Travail à faire :
Quelle distance doit-il obtenir lorsqu’il mesure la diagonale D de son rectangle ?
✎ Travail n° 2 Pythagore 2
Vous souhaitez repeindre le plafond d’un abri dont le plan est donné ci-dessous.
Vous ne disposez pas d’échelle, qui vous permettrait de mesurer directement le plafond, mais d’un télémètre laser qui vous permet de mesurer les distances reportées sur le plan.
🎯 Travail à faire :
À partir de ces mesures, déterminer la surface (en m2) du plafond de façon à savoir combien de peinture il faudra acheter.
✎ Travail n° 3 Rapports trigonométriques
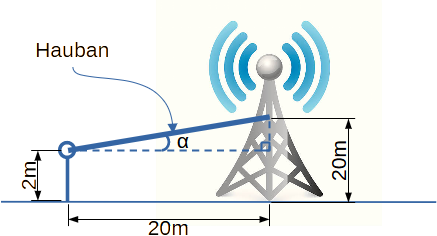
Une antenne hertzienne est maintenue verticale à l’aide de haubans métalliques.
L’arrimage d’un des haubans est représenté ci-dessous :
🎯 Travail à faire :
-
Déterminer la valeur de l’angle α (en degrés) que fait le hauban avec l’horizontale ?
Réponse
-
Pour une bonne stabilité, l’angle α doit être au minimum de 45°.
À quelle hauteur minimale de l’antenne faudrait-il arrimer le hauban pour répondre à cette exigence ?
Réponse
✎ Travail n° 4 Loi du cosinus
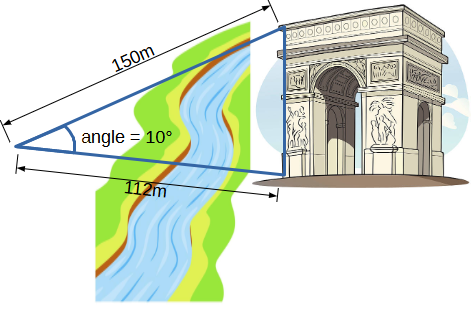
Vous voulez déterminer la hauteur d’un monument situé sur l’autre rive d’un fleuve au bord duquel vous vous tenez.
Un télémètre laser vous permet de mesurer les distances qui vous séparent du pied et du sommet du monument mais aussi l’angle entre celles-ci.
|
Le triangle formé par les 2 longueurs mesurées et la hauteur du monument n’est pas rectangle. |
🎯 Travail à faire :
Déterminer la hauteur du monument.
✎ Travail n° 5 Loi du sinus[1]
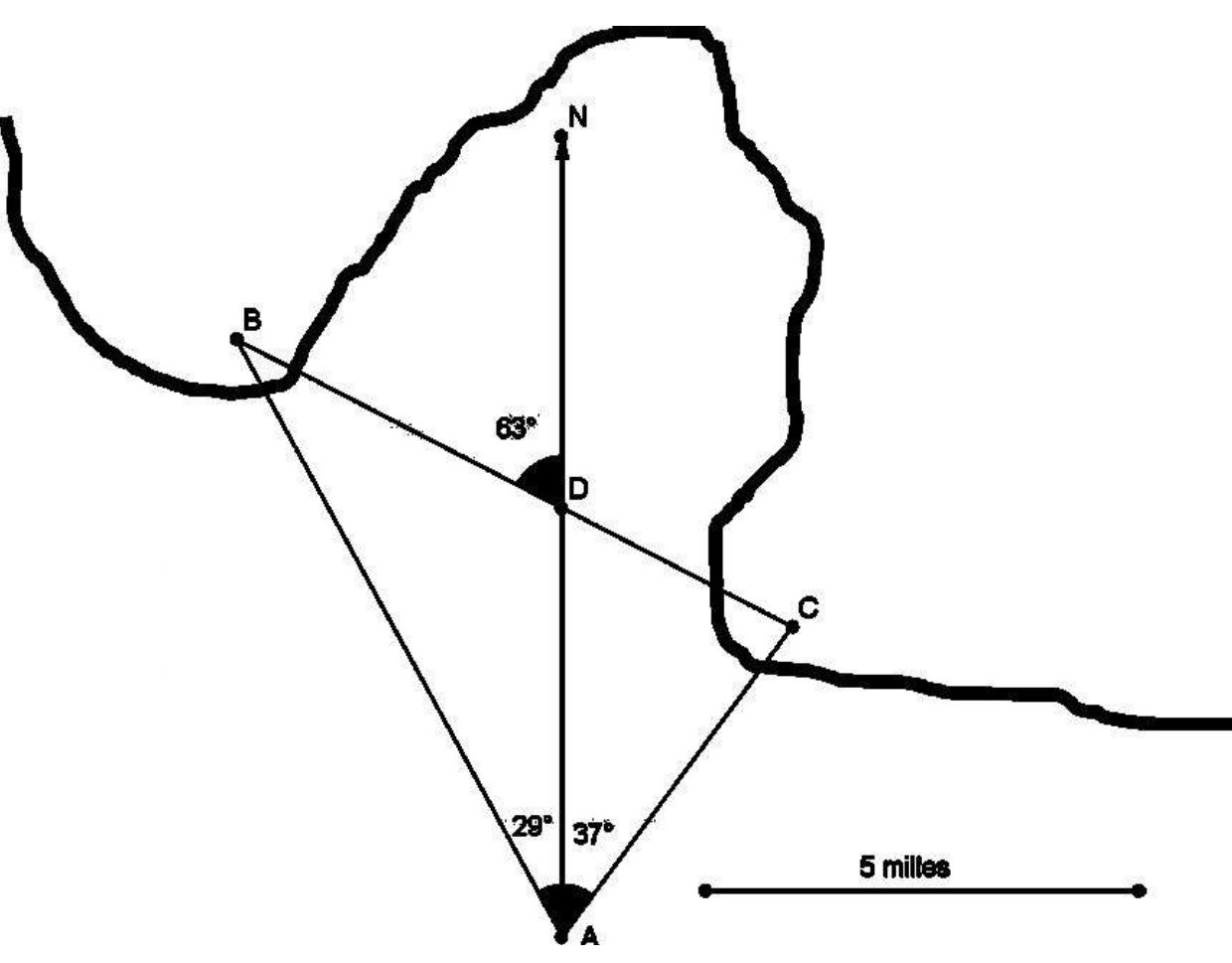
Un voilier (A) s’approche de côtes françaises qui sont balisées par 2 phares (B et C).
Le marin lit sur sa carte marine que les phares sont éloignés de 7,2 milles marins (BC = 7,2 milles marins).
Depuis le voilier, le marin relève le phare B au cap 29° Ouest et le phare C au cap 37° Est.
Sur la carte, il détermine que le phare B est au cap 63° Ouest depuis le phare C.
🎯 Travail à faire :
Calculer les distances AB et AC en milles marins et en kms (1 mille marin = 1852m).
|
La somme des angles d’un triangle vaut toujours 180°. |
🞄 🞄 🞄