Codage des nombres à virgule
Virgule fixe et virgule flottante
Il existe deux codages binaires des nombres à virgule :
-
le codage en virgule fixe
-
le codage en virgule flottante .
Le codage en virgule fixe est encore utilisé dans certains microcontrôleurs.
Le codage en virgule flottante est utilisé partout ailleurs : ordinateurs, smartphones …
L’idée du codage en virgule fixe est de retenir un nombre fixe de chiffres après la virgule.
Dans le cas du codage en virgule flottante, on retient un nombre fixe de chiffres significatifs (beaucoup de chiffres après la virgule pour les petits nombres, et beaucoup de chiffres avant la virgule pour les grands nombres).
Virgule fixe
Dans cette représentation, le développeur informatique doit :
-
décider le nombre total de bits utilisés pour coder la valeur du nombre
-
décider le nombre de bits utilisés pour coder la partie entière et la partie décimale (→ la précision)
-
coder la partie entière sur le nombre de bits choisi pour la représenter en utilisant les puissances positives de 2
-
coder la partie décimale sur le reste des bits en utilisant les puissances de 2 négatives (2-1=1/2=0.5, 2-2=1/4=0.25, 2-3=1/8=0.125, 2-4=1/16=0.0625 …)
Puissances de 2 |
22 |
21 |
20 |
2-1 |
2-2 |
2-3 |
2-4 |
|
Écriture binaire |
1 |
0 |
1 |
, |
1 |
1 |
0 |
1 |
⇒ 1011101|2 = 1 x 22 + 1 x 20 + 1 x 2-1 + 1 x 2-2 + 1 x 2-4
= 4 + 1 + 0.5 + 0.25 + 0.0625
= 5.8125|
Méthode pour coder la partie décimale
Pour coder la partie décimale on peut utiliser la méthode des multiplications successives :
La représentation binaire de la partie décimale du nombre de départ est alors la suite des parties entières des multiplications successives Ex. pour la partie décimale de l’exemple précédent (→ 5.8125):
⇒ 0,8125|10 = 1101|2 |
La représentation en virgule fixe est très efficace car les calculs aux niveau du processeur (addition, soustraction multiplication, division) se basent sur les entiers.
Par contre, elle n’offre qu’une précision limitée si on choisit un nombre restreint de bits pour la partie décimale (→ ex. : précision de 0,5 pour 1 bit à comparer avec le système décimal pour lequel un chiffre après la virgule offre une précision de 0,1).
|
Voir Decimal/Binary Converter |
Virgule flottante
La représentation en virgule flottante est la plus répandue et se base sur une norme, l'IEEE-754, qui propose une représentation en simple, double ou quadruple précision sur, respectivement, 32, 64 ou 128 bits.
Dans cette représentation :
-
1 bit est utilisé pour coder le signe ( ‘+’ → 0, ‘-’ → 1)
-
un ensemble de bits (8, 11 ou 15 selon la précision) codent un exposant
-
le reste des bits (23, 52 ou 113 selon la précision) codent ce qu’on appelle la mantisse (ou plus rarement le significande)
C’est l’expression d’une partie décimale codée avec des puissances de 2 négatives comme dans la représentation à virgule fixe
La valeur du nombre réel est alors :
réelIEEE754 = (-1)signe x ( 1 + mantisse) x 2exposant - biais |
Le biais est une constante valant respectivement 127, 1023, 16383 en simple, double et quadruple précision
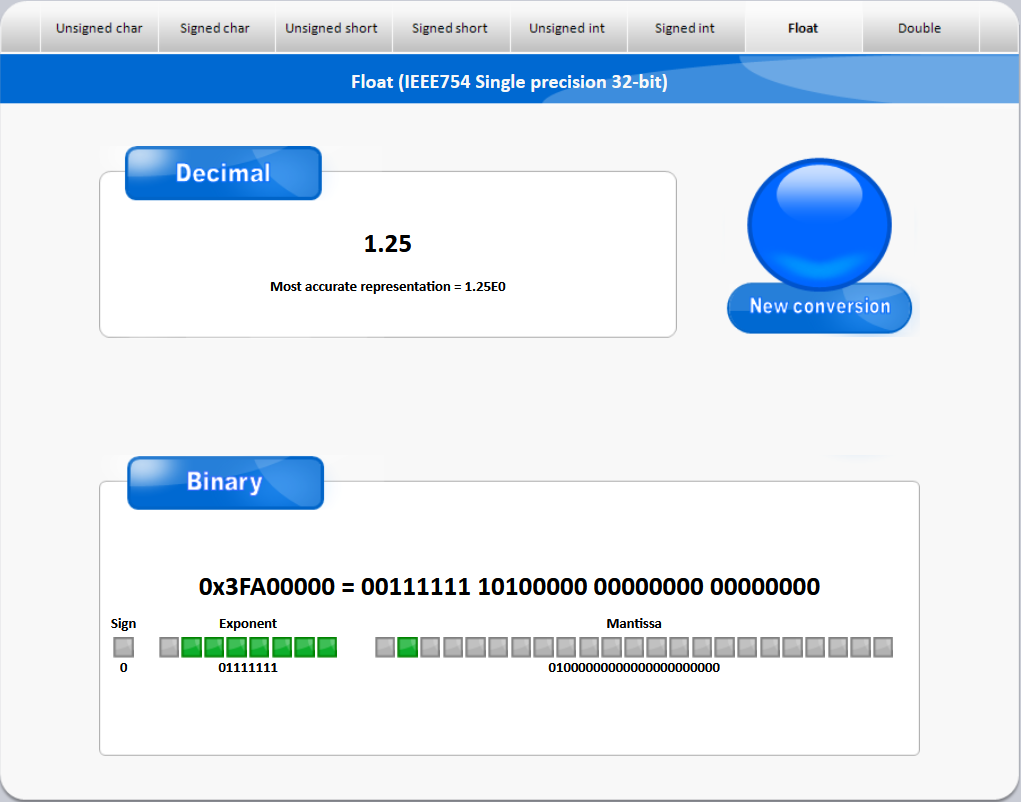
Exemple de représentation IEEE754 simple précision de la valeur +1.25 sur le convertisseur en ligne Online Binary-Decimal Converter :
-
le signe vaut 0
-
l’exposant vaut 127 (← 01111111|2)
-
la mantisse vaut 0.25 (← 01000…|2 ⇒ 1 x 2-2)
⇒ au final on a bien (-1)0 x (1 + 0.25) x (2127 - 127) = 1 x 1.25 x 20 = 1 x 1.25 x 1 = 1.25
Outre une précision appréciable et une prise en charge complète par les langages de programmation, la représentation IEEE754 offre également la possibilité de coder des valeurs “spéciales” :
-
+∞ et -∞
-
NaN pout Not a Number. C’est une valeur qui indique le résultat d’une opération arithmétique invalide comme 0/0, ∞ - ∞, ∞ / ∞ …
Pour aller plus loin sur la représentation IEEE754, consulter la vidéo ci-dessous :
Les nombres à virgule sont approchés
|
Quel que soit le codage choisi (virgule fixe ou flottante), un problème demeure : si le nombre a une écriture infinie en base 2, il ne peut pas être représenté dans un ordinateur puisqu’il le stocke avec un nombre fini de bits (8, 16, 32 …). Le nombre manipulé par la machine n’est alors qu’une valeur approchée du nombre réel. |
Exemples de calculs menant à des résultats surprenants du fait de la représentation approchée des nombres réels :
Python 3.11.4 | packaged by Anaconda, Inc. | (main, Jul 5 2023, 13:47:18) [MSC v.1916 64 bit (AMD64)] on win32
Type "help", "copyright", "credits" or "license" for more information.
>>> 0.5 - 0.2 - 0.2 - 0.1
-2.7755575615628914e-17
>>>>>> 9007199254740992.0 + 1.0 == 9007199254740992.0 (1)
True (2)| 1 | on teste si (N+1) est égal à N … |
| 2 | … et Python nous dit étonnamment que oui !! |
>>> 1.0 + 1.0 + 9007199254740992.0
9007199254740994.0 (1)
>>> 9007199254740992.0 + 1.0 + 1.0
9007199254740992.0 (1)| 1 | le même calcul mène à des résultats différents |
🞄 🞄 🞄