Étude de la propagation d’une épidémie[1]
Présentation
Cet atelier vise à modéliser sous forme de suite numérique et étudier la propagation d’une maladie sur une population sachant que :
-
Un individu sain est un individu n’ayant jamais été touché par la maladie.
-
Un individu malade est un individu qui a été touché par la maladie et non guéri.
-
Un individu guéri est un individu qui a été touché par la maladie et qui a guéri.
-
Une fois guéri, un individu est immunisé et ne peut plus tomber malade.
-
Les premières observations montrent que, d’un jour au suivant :
-
5% des individus sains tombent malades.
-
20% des individus malades guérissent.
-
✎ Travail n° 1 Application numérique
🕮 Énoncé
Pour tout entier naturel n, on note an , la proportion d’individus sains n jours après le début de l’expérience et bn la proportion d’individus malades n jours après le début de l’expérience.
On suppose qu’au début de l’expérience tous les individus sont sains : a0 = 1 et b0 = 0.
🎯 Travail à faire :
-
Calculer a1 et b1.
-
Montrer que a2 = 0.9025 et b2 = 0.0875.
-
Exprimer an+1 en fonction de an.
En déduire la nature de la suite (an) et l’expression de an en fonction de n. -
Exprimer bn+1 en fonction de an et bn.
💻 Travail n° 2 Approche informatique
🎯 Travail à faire :
-
Proposer un algorithme qui permet de déterminer le pic de l’épidémie sur une période de 100 jours et le coder en Python
Solution
pic-epidemie.pyperiode = 100 sains = [1] malades = [0] for jourPrecedent in range(periode) : sains.append(sains[jourPrecedent]*0.95) malades.append(malades[jourPrecedent] * 0.8 + sains[jourPrecedent] * 0.05) print(f"Pic de l'épidémie atteint au jour n° {malades.index(max(malades))}") -
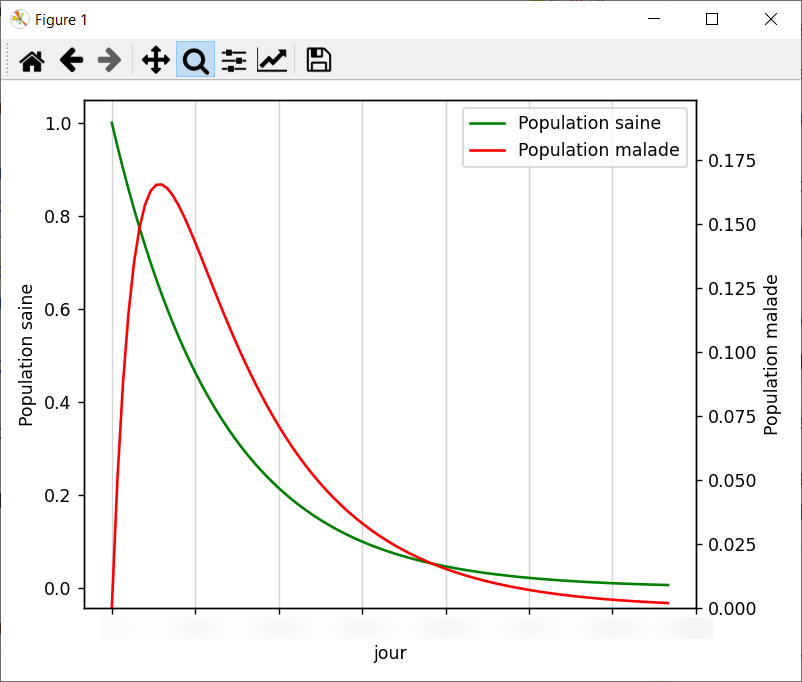
Faire un script Python qui trace l’évolution de la population saine et de la population malade.
Vérifier graphiquement le jour du pic de l’épidémieSolution
suite-epidemie-courbe.pyimport matplotlib.pyplot as plt import matplotlib.ticker as ticker print(">>>> Etude de la propagation d'une maladie <<<<\n"); # Saisie valeur initiale periodeEtude = int(input("Saisir la période d'étude en nombres de jours : ")) # Calcul des termes de la suite sains = [1] malades = [0] for jourPrecedent in range(periodeEtude) : sains.append(sains[jourPrecedent]*0.95) malades.append(malades[jourPrecedent] * 0.8 + sains[jourPrecedent] * 0.05) # Création d'une figure fig = plt.figure() # Ajout des courbes de population saine et malade dans la figure courbeSains = fig.add_subplot(1 # nrows , 1 # ncols , 1 # index , xscale='linear' ) courbeSains.set_xlabel('jour') courbeSains.set_ylabel('Population saine') courbeMalades = courbeSains.twinx() # 2ème courbe qui partage le même axe des x mais pas celui des y courbeMalades.set_ylabel('Population malade') # Tracé des courbes courbeSains.xaxis.set_major_locator(ticker.MaxNLocator(integer = True)) plotSains = courbeSains.plot(range(periodeEtude+1), sains, label="Population saine", color="green") courbeMalades.set_ylim(top=max(malades)*1.2) plotMalades = courbeMalades.plot(range(periodeEtude+1), malades, label="Population malade", color="red") # Mise en place des légendes courbes = plotSains + plotMalades legendes = [c.get_label() for c in courbes] courbeSains.legend(courbes, legendes, loc=0) # Configuration des grilles courbeSains.grid(which='major', axis='x', color='lightgray') # Affichage de la courbe plt.tight_layout() plt.show()
🞄 🞄 🞄