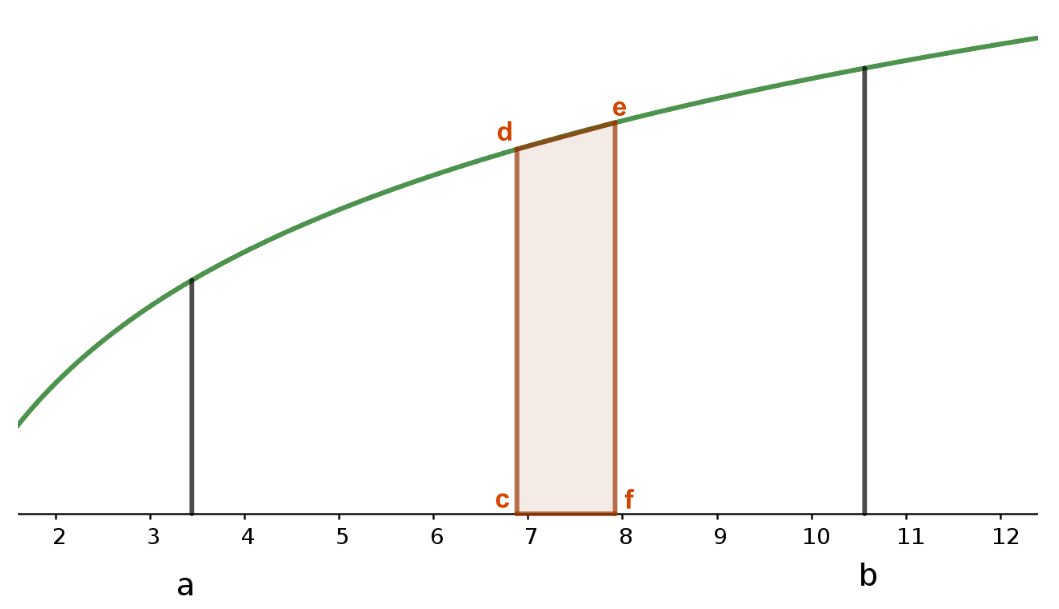
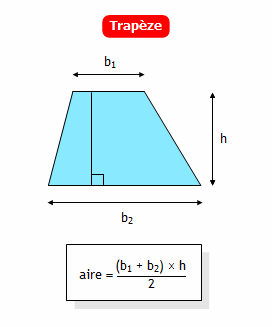
Calcul d’une intégrale avec la méthode des trapèzes
Crédits[1]
Application
💻 Travail n° 1
🎯 Travail à faire :
-
Utiliser Python pour calculer la même chose.
-
Faire évoluer le script Python pour permettre de calculer cette même intégrale mais en proposant cette-fois-ci à l’utilisateur de saisir :
-
la borne inférieure de l’intégrale
-
la borne supérieure de l’intégrale
-
le nombre de points/trapèzes à utiliser pour calculer l’intégrale
Vérifier les résultats obtenus.
-
Utiliser la fonction
linspace()du module Numpy pour définir un tableau contenant un ensemble de valeurs également réparties entre 2 nombres. -
On peut appliquer une fonction sur un tableau Numpy. Le résultat retourné est alors l’ensemble des images de chacun des points du tableau à travers la fonction.
def f(x) : return x/2 abscisses = np.linspace(0,1,5) (1) ordonnees = f(abscisses) (2) print(ordonnees) # Affiche : # [0. 0.125 0.25 0.375 0.5 ]1 création d’un tableau contenant 5 points également répartis entre 0 et 1 (→ [0,0.25,0.5,0.75,1]) 2 Application de la fonction f(x)=x/2 à l’ensemble des points du tableau abscisses
-
-
💻 Travail n° 2
🎯 Travail à faire :
-
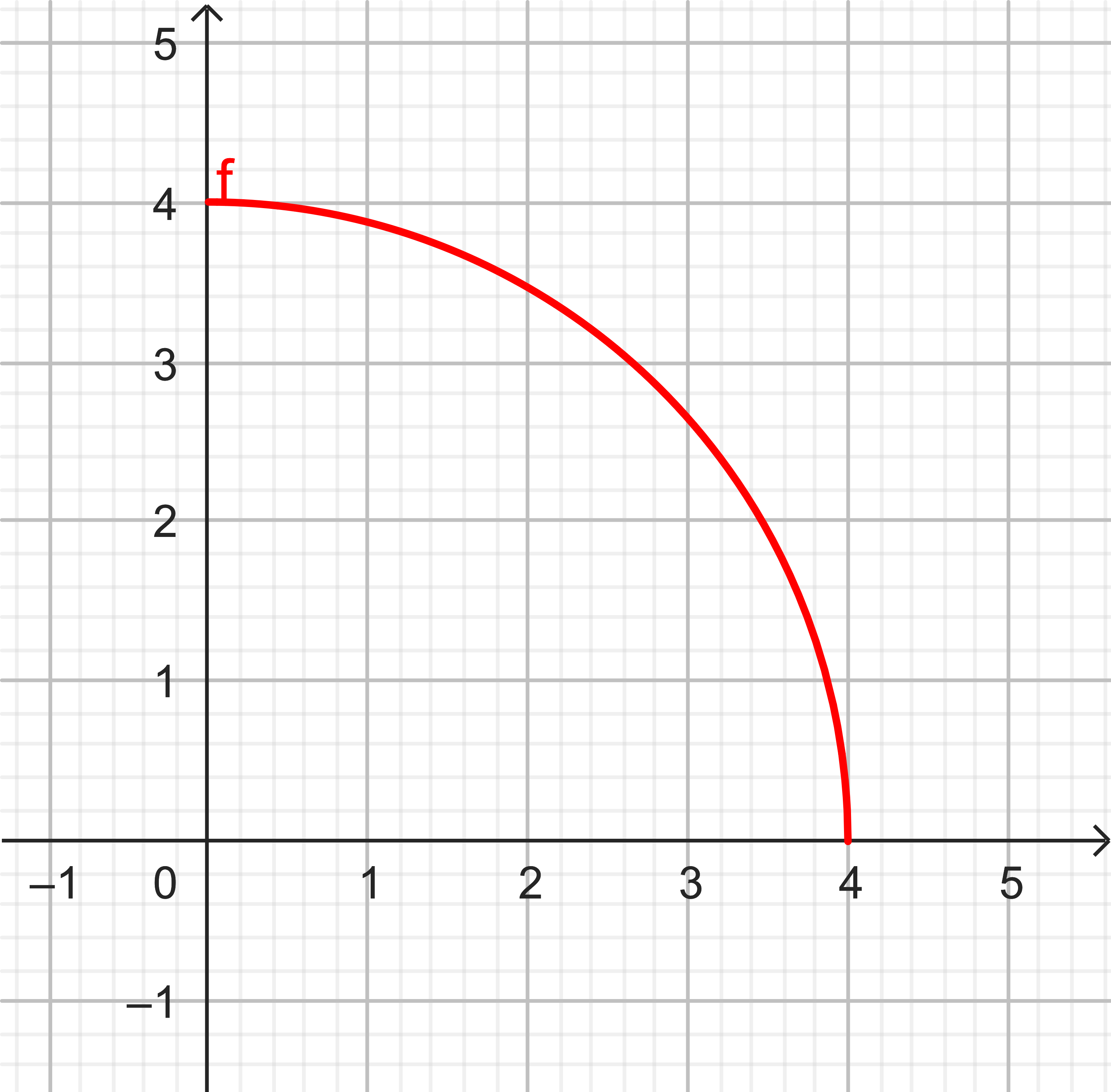
Comparer le résultat avec une propriété de géométrie vue au collège.
-
Déterminer par programmation en combien d’intervalles on doit découper la courbe pour obtenir, avec la méthode des trapèzes, un résultat avec une précision de ±1% par rapport au résultat théorique.
🞄 🞄 🞄