Fonctions affines

✎ Travail n° 1 Rappels

🎯 Travail à faire :

Faire le TD Fonctions affines / Droites du plan pdf[1]

✎ Travail n° 2 Évolution de la taille d’une base de données

On considère une base de données SQLite nommée dummy.sqlite que l’on met à jour toutes les minutes.

Même si elle ne contient pas de données au départ sa taille n’est pas nulle puisqu’elle contient des informations sur les tables qui la composent.

Le resultat de la commande ls -l le confirme :

localhost:~ # ls -l dummy.sqlite
-rw-r--r-- 1 root root 8192 Oct  1 10:03 dummy.sqlite (1)
1 même vide de données, notre base de données occupe 8192 octets sur le disque

L’évolution de sa taille peut être affichée périodiquement avec la commande suivante :

watch -n 60 ls -l dummy.sqlite (1)
1 Affiche toutes les 60s le résultat de la commande ls -l dummy.sqlite qui renseigne — entre autres — sur la taille du fichier dummy.sqlite (→ 5ème colonne).

Le résultat de cette commande appliquée à notre base de données donne :

Every 60.0s: ls -l dummy.sqlite         localhost: Tue Oct  1 10:20:27 2024
-rw-r--r-- 1 0 0 8192 Oct  1 10:20 dummy.sqlite
-rw-r--r-- 1 0 0 24576 Oct  1 10:21 dummy.sqlite (1)
-rw-r--r-- 1 0 0 40960 Oct  1 10:22 dummy.sqlite (1)
-rw-r--r-- 1 0 0 57344 Oct  1 10:23 dummy.sqlite (1)
1 l’heure de mise à jour de la base de données apparait dans la 8ème colonne (→ 10:21, 10:22…​)

🎯 Travail à faire :

  1. De combien d’octets évolue la taille de la base de données toutes les minutes ?

  2. En déduire l’équation qui détermine la place occupée en octets sur le disque en fonction du temps (en minutes).

  3. Quelle sera la taille de la base de données au bout de 2 heures et 30 minutes ?

  4. Au bout de combien d’heures la base de données occupera plus de 10Moctets ?

  5. Exprimer ce temps en heures/minutes/secondes

💻 Travail n° 3 Transformation affine

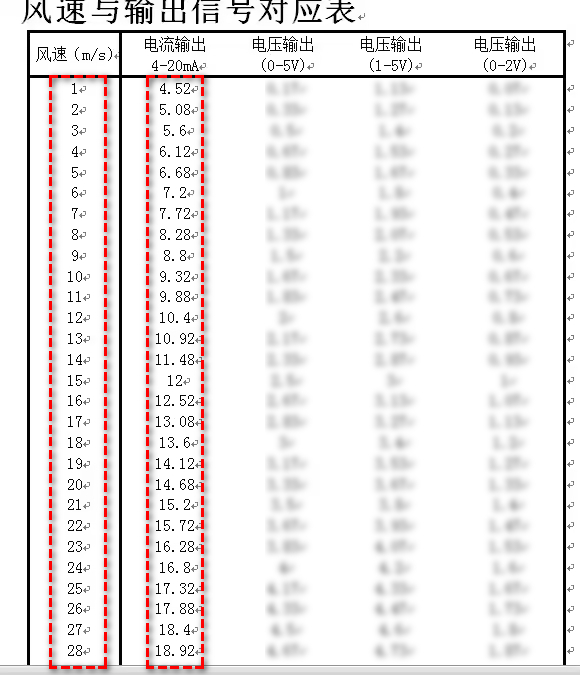
On dispose des caractéristiques d’un capteur qui donne une image de la vitesse du vent (en m.s-1) sous forme d’une valeur de courant (en mA).

capteur vent

🎯 Travail à faire :

  1. Sur Geogebra ou Excel, tracer les points qui représentent la vitesse du vent en fonction du courant délivré par le capteur.

    Pour éviter d’avoir à retaper les valeurs, on vous donne le fichier capteur-vent.csv xls(→ coma separated values) qui contient toutes les données du tableau.

    • Dans Excel, importer les données depuis le menu Données  Obtenir des données  à partir d’un fichier texte/csv

    • Dans Geogebra, l’importation des données se fait en cliquant droit sur la cellule A1 du tableur puis en sélectionnant “Importer un fichier de données”

  2. À quelle fonction mathématique peut-on assimiler ce nuage de points ?

  3. En posant :
    Vmin = 1 m.s-1
    Vmax = 28 m.s-1
    Imin = 4.52 mA
    Imax = 18.92 mA

    déterminer l’expression générale de cette fonction en détaillant le calcul.

    Réponse finale attendue :

    L’expression simplifiée de la fonction est :

    transformation lineaire

    • le coefficient directeur d’une droite est défini comme le rapport entre la variation verticale (différence des ordonnées) et la variation horizontale (différence des abscisses) entre deux points distincts de la droite.

    • Connaissant les coordonnées (x1, y1) d’un point appartenant à une droite, l’ordonnée à l’origine ‘b’ est déterminée par :
      b = y1 - a . x1
      (‘a’ étant le coefficient directeur de la droite)

  4. Vérifier que l’expression de cette fonction est conforme à ce qu’arrive à déterminer Géogebra (→ “Modèle d’ajustement linéaire”) ou Excel (→ “Courbe de tendance linéaire” avec option “Afficher l’équation sur le graphique” cochée)

  5. Écrire un script Python qui :

    • charge les points de mesure du capteur du fichier capteur-vent.csv xls

    • détermine le coefficient directeur et l’ordonnée à l’origine de la droite affine qui permet d’obtenir la vitesse du vent à partir du courant délivré par le capteur (← v = a . i + b)

    • trace la droite affine ET le nuage de points contenu dans capteur-vent.csv xls

      1. Le chargement d’un fichier .csv dans un tableau Numpy peut se faire avec la fonction np.loadtext()

      2. On vous donne le source d’un script qui trace :

        • une fonction linéaire : y = 2 . x

        • un ensemble de points définis manuellement

        import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__":
    # 1. Définir manuellement les données
    donnees = np.array([[0,2], [1,3], [2,4], [3,5], [4,6], [5,7], [6,8], [7,9], [8,10], [9,11], [10,12]])

    # 2. Calculer les valeurs minimales et maximales (On considère que les points sont triés)
    Xmin = donnees[0][0]
    Ymin = donnees[0][1]
    Xmax = donnees[-1][0]
    Ymax = donnees[-1][1]

    # 3. Définir la plage de la fonction linéaire
    x = np.linspace(0, 10, 100)

    # 4. Définir la fonction linéaire: y = f(x)
    y = 2 * x

    # 5. Tracer les courbes : points de mesure (en vert) et fonction linéaire (en rouge)
    # . Création d'une figure avec un seul tracé
    fig,ax = plt.subplots()

    # . Configuration de la grille :
    ax.grid(which='both', color='#CCCCCC', linestyle='--')

    # . Nommage du graphique
    ax.set_title("Graphique de démonstration")

    # . Nommage des axes
    ax.set_xlabel("$x$")
    ax.set_ylabel("$y$")

    # . Tracé des courbes
    ax.plot(donnees[:,0], donnees[:,1],'g.') # points de mesure
    ax.plot(y, x,'r-') # fonction linéaire

    # . Ajout de la légende
    ax.legend(["Points de mesure", "$y = 2 \\cdot x$"], loc="lower right")

    # . Affichage des valeurs minimales et maximales
    ax.text(Xmin,Ymin, f"({Xmin},{Ymin})", fontsize=9, ha='left', va="top")
    ax.text(Xmax, Ymax, f"({Xmax},{Ymax})", fontsize=9, ha='right', va="bottom")

    # . Affichage de la figure
    plt.show()

  6. Faire évoluer le script pour qu’il ne considère pas que les points de mesure du fichier .csv sont triés

    Les fonctions np.min() et np.max() permettent d’obtenir le minimum et le maximum d’un tableau Numpy selon un certain axe.

✎ Travail n° 4 Loi de Moore

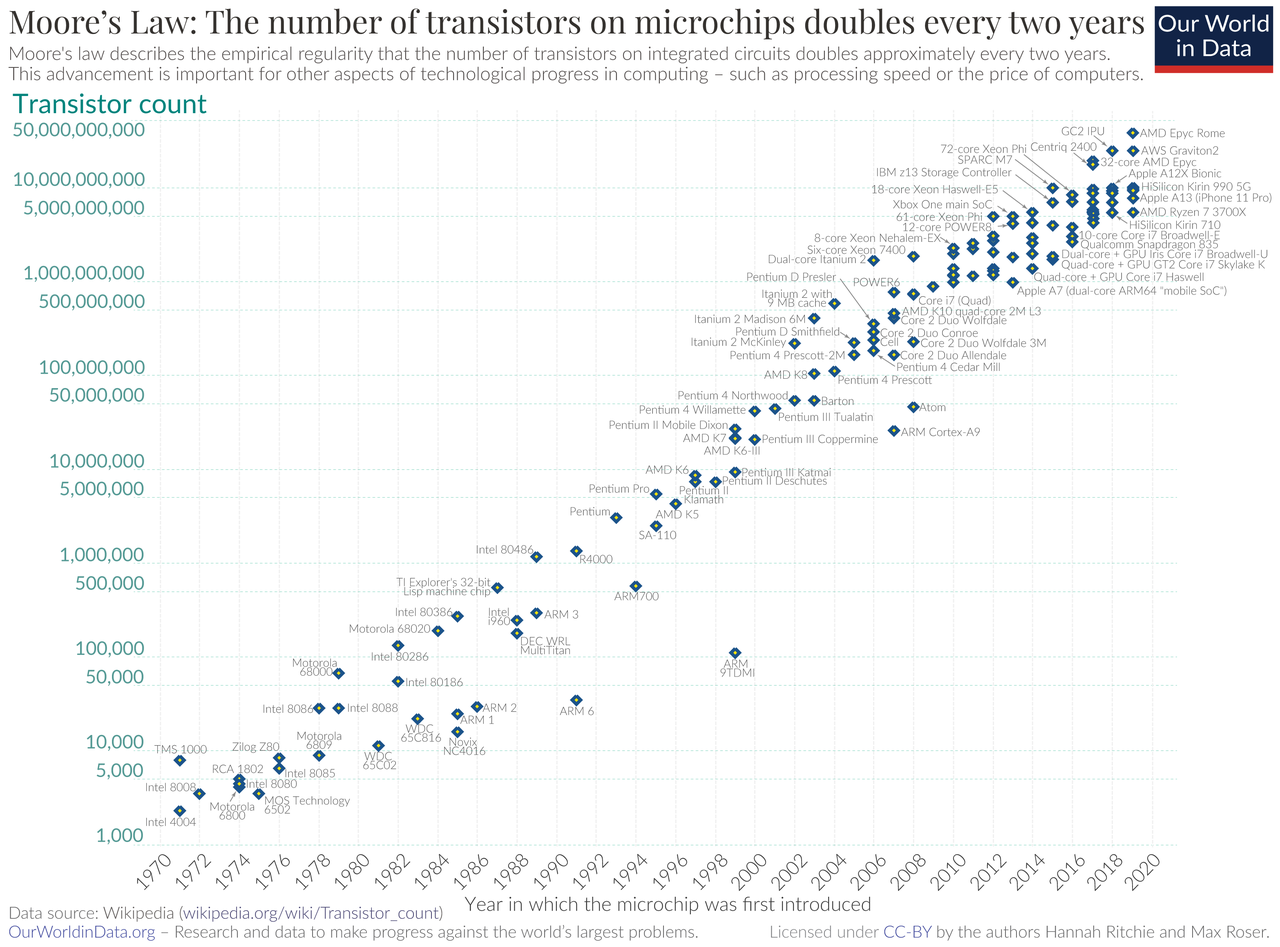
En 1975, Gordon Moore (03/01/1929 → ✝ 24/03/2023) — co-fondateur d'Intel — émit une prédiction qui prévoyait approximativement le doublement du nombre de transistors dans les microprocesseurs tous les 2 ans.

Bien qu’empirique, cette prédiction s’est vérifiée pendant près de 40 ans.

🎯 Travail à faire :

  1. Sachant que le microprocesseur i960 d’Intel sorti en 1988 comportait environ 250000 transistors, quel est l’ordre de grandeur du nombre de transistors sur le Pentium 4 Prescott, toujours d'Intel, sorti en 2004 ?

  2. Vérifier visuellement votre résultat sur le graphique ci-dessous :

    loi moore 1970 2020
    Figure 1. Un graphique semi-logarithmique du nombre de transistors pour les microprocesseurs par rapport aux dates d’introduction, doublant presque tous les deux ans. (Source : Wikipedia)

  3. Selon vous, quel est l’intérêt d’utiliser sur le graphique un axe logarithmique pour le nombre de transistors ?

    L’allure du graphe serait-elle restée une droite si on avait utilisé une graduation linéaire sur l’axe des ordonnées ?

  4. Par calcul, en quelle année a-t-on atteint 10 milliards de transistors sur un microprocesseur ?

  5. Vérifier visuellement votre résultat sur le graphique reproduit plus haut.

1. Sujet rédigé par P. Meyer

🞄  🞄  🞄